Group A

$3\times4=12$

(Answer any four questions)

1. Define tautology, contradiction and satisfiable with an example.

Tautology: In propositional logic we define a term tautology for a compound statement, such that its truth value is always true for all possible combinations. Example $(p\wedge q)\rightarrow(p\vee q)$, is a tautologic expression.

Contradiction: In propositional logic, we define a term contradiction for a compound statement, such that its truth vaule is always false for all possible combinations. Example $\neg(\neg(p\wedge q)\leftrightarrow(\neg p\vee\neg q))$, is a contradictory statement.

Satisfiable: In propositional logic, a compound statement is satisfiable, if there exists atleast one combination such that, the compound statement evaluates to true. Example $A\wedge\neg B$ is true when $A=T$, and $B=F$, thereby making them solution for satisfiability.

2. Represent the statement "It is raining and I will not go to college." using propositional logic.

Breaking the compound statement into two propositions:

• $P$: It is raining.
• $Q$: I will go to college.

The above compound statement can be written as: $P\wedge\neg Q$.

3. Prove that in a graph the number of vertices of odd degree is always even.

Expressing the total number of vertices in terms of vertices with odd degrees and vertices with even degrees:

$$\begin{align*} \sum^n_{i=1}{n_i}=\sum_{\text{even}}{n_i}+\sum_{\text{odd}}{n_i} \end{align*}$$

We know that the total degree of a graph is twice the number of edges $e$. Therefore the above expression can be written as:

$$2\cdot e=\sum_{\text{even}}{n_i}+\sum_{\text{odd}}{n_i}$$

Now, the expression on the left hand side, i.e., $2\cdot e$ is always even. The first expression on the right hand side, $\sum_{\text{even}}{n_i}$ is always even as it is the sum of even numbers.

Therefore, the sum of odd degrees, $\sum_{\text{odd}}{n_i}$, is nothing but the difference between two even numbers, hence it is always even.

4. Find the generating function for the sequence $\{0,0,1,1,1\ldots\}$.

5. A committee of $7$ members is to be chosen from $6$ artists, $4$ singers and $5$ writers. In how many ways can this be done if in the committee there must be at least one member from each group and at least $3$ artists?

6. Prove using Venn diagram: $(B-A)\cup(C-A)=(B\cup C)-A$.

The given expression is $(B-A)\cup(C-A)=(B\cup C)-A$.

The expression on the left hand side contains the union of all elements that are present in $B$ but not in $A$, and all elements that are present in $C$ but not in $A$. The Venn diagram is:

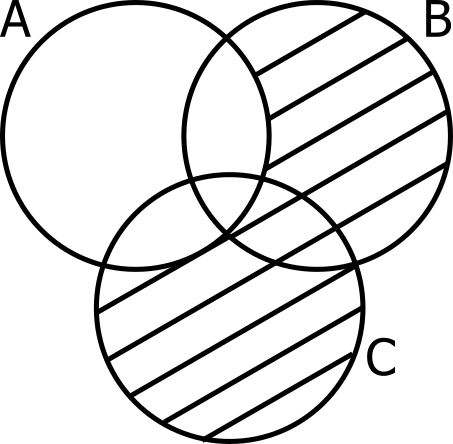
The expression on the right hand side contains all elements that are present in $B$ and $C$ but not in $A$. The Venn diagram is:

---

Group B

$6\times4=24$

(Answer any four questions)

7. Prove the following logic argument: If horses fly or cows eat grass, then the mosquito is the national bird. If the mosquito is the national bird then peanut butter tastes good on hot dogs. But peanut butter tastes terrible on hot dogs. Therefore, cows don't eat grass.

Breaking the above compound statements into propositions:

• $p$: Horses fly.
• $q$: Cows eat grass.
• $r$: Mosquito is the national bird.
• $s$: Peanut butter tastes good on hot dogs.

As per the question, the first compound statement is: $(p\vee q)\rightarrow r$

The second compound statement that can be brought out is: $r\rightarrow s$

Relating the two compound statements using hypothetical syllogism, we get:

$$\begin{align*} &(p\vee q)\rightarrow r\\ &r\rightarrow s\\ &-------\\ &\therefore (p\vee q)\rightarrow s \end{align*}$$

Inverting the above result, we get: $\neg s\rightarrow\neg(p\vee q)$

Relating the above result with the third compound statement $\neg s$, using Modus Ponen's, we get:

$$\begin{align*} &\neg s\rightarrow\neg(p\vee q)\\ &\neg s\\ &-------\\ &\therefore \neg(p\vee q) \end{align*}$$

The above result can be written as: $\neg p\wedge\neg q$. Applying simplification, on the result we get: $\neg q$, which translates to "Cows don't eat grass".

8. A new flag is to be designed for your college; it should have $6$ vertical strips using four colors. In how many ways can this be done such that no two adjacent strips should have the same color?

9. Solve the recurrence relation: $a_n=a_{n-1}+2a_{n-2}$ with $a_0=2$ and $a_1=7$.

Given relation:

$$a_n=a_{n-1}+2a_{n-2}$$

The above is an example of homogenous recurrence relation. We can find the characteristic equation by replacing $a_n=r^n$. Therefore, we get:

$$\begin{align*} &r^n=r^{n-1}+2r^{n-2}\\ \Rightarrow\ &r^n-r^{n-1}-2r^{n-2}=0\\ \end{align*}$$

On dividing both sides with $r^{n-2}$, we get:

$$\begin{align*} &r^2-r-2=0\\ \Rightarrow\ &r^2-2r+r-2=0\\ \Rightarrow\ &r(r-2)+(r-2)=0\\ \Rightarrow\ &r=-1,2 \end{align*}$$

Since the roots found are different, therefore the solution equation can be found out using:

$$a_n=A_1r_1^n+A_2r_2^n$$

We know $a_0=2$:

$$\begin{align*} &a_0=A_1(-1)^0+A_2\cdot 2^0\\ \Rightarrow\ &A_1+A_2=2&&&&&&&&&&(1) \end{align*}$$

We know $a_1=7$:

$$\begin{align*} &a_1=A_1(-1)^1+A_2\cdot 2^1\\ \Rightarrow\ &-A_1+2A_2=7&&&&&&&&&&(2) \end{align*}$$

On adding equations (1) and (2), we get:

$$3A_2=9\Rightarrow A_2=3$$

And putting the value of $A_2$ in (1), we get: $A_1=-1$.

Therefore, the solution for the given recurrence relation is:

$$a_n=-1\cdot(-1)^n+3\cdot2^n$$

10. Let $f:A\rightarrow B$ and $g:B\rightarrow C$ be bijective then show that the relation $(g\circ f)^{-1}=f^{-1}\circ g^{-1}$ holds true.

11. Prove using mathematical induction $1^2+2^2+3^2+\ldots+n^2=\frac{n(n+1)(2n+1)}6$.

Given relation:

$$1^2+2^2+3^2+\ldots+n^2=\frac{n(n+1)(2n+1)}6$$

Solving the basis:

$n$	LHS	RHS
$1$	$1^2=1$	$\frac{1\cdot2\cdot3}{6}=1$
$2$	$1^2+2^2=5$	$\frac{2\cdot3\cdot5}{6}=5$

Therefore, the basis holds true. For $n=k$:

$$\begin{align*} 1^2+2^2+3^2+\ldots+k^2=\frac{k(k+1)(2k+1)}{6}&&&&&&&&&&(1) \end{align*}$$

For $n=k+1$:

$$\begin{align*} \text{LHS}&=1^2+2^2+3^2+\ldots+k^2+(k+1)^2\\ &=\frac{k(k+1)(2k+1)}{6}+(k+1)^2&&[\text{From eq. (1)}]\\ &=(k+1)\left[\frac{k(2k+1)+6(k+1)}{6}\right]\\ &=(k+1)\left[\frac{2k^2+7k+6}{6}\right]\\ &=(k+1)\left[\frac{2k^2+4k+3k+6}{6}\right]\\ &=(k+1)\left[\frac{2k(k+2)+3(k+2)}{6}\right]\\ &=\frac{(k+1)(k+2)(2k+3)}{6}\\\\ \text{RHS}&=\frac{(k+1)[(k+1)+1][2(k+1)+1]}{6}\\ &=\frac{(k+1)(k+2)(2k+3)}{6} \end{align*}$$

Since, $\text{LHS}=\text{RHS}$, therefore through mathematical induction, the given equation holds true.

12. Explain the steps to determine the planarity of a graph.

---

Group C

$6\times2=12$

(Answer any four questions)

13. Prove using mathematical induction:

$$\bold{1+4+7+\ldots+(3n-2)=\frac{n(3n-1)}{2}, n\in\N}$$

Given equation:

$$1+4+7+\ldots+(3n-2)=\frac{n(3n-1)}{2}, n\in\N$$

Solving the basis:

$n$	LHS	RHS
$1$	$1$	$\frac{1\cdot2}{2}=1$
$2$	$1+4=5$	$\frac{2\cdot5}{2}=5$

Therefore, the basis holds true. For $n=k$:

$$\begin{align*} 1+4+7+\ldots+(3k-2)=\frac{k(3k-1)}{2}&&&&&&&&&&(1) \end{align*}$$

For $n=k+1$:

$$\begin{align*} \text{LHS}&=1+4+7+\ldots+(3k-2)+(3k+1)\\ &=\frac{k(3k-1)}{2}+(3k+1)&&[\text{From eq. (1)}]\\ &=\frac{3k^2+5k+2}{2}\\ &=\frac{3k^2+3k+2k+2}{2}\\ &=\frac{3k(k+1)+2(k+1)}{2}\\ &=\frac{(k+1)(3k+2)}{2}\\\\ \text{RHS}&=\frac{(k+1)[3(k+1)-1]}{2}\\ &=\frac{(k+1)(3k+2)}{2} \end{align*}$$

Since $\text{LHS}=\text{RHS}$, therefore the above equation holds true for all values of $n$, where $n\in\N$.

14. If $f:Z\times Z\rightarrow Z$, where Z is the set of integers and the relation $f(x,y)=x*y=x+y-xy$. Prove that the binary operation $*$ is commutative and associative, also find the identity element and inverse of each element.

Depreciated — Not in syllabus.

15. Prove that in a simple graph with $n$ vertices and $k$ components can have utmost $(n-k)(n-k+1)/2$ edges.

Let us consider a graph $G$, where the number of vertices in each of the $k$ components be $n_1, n_2, \ldots, n_k$. Thus we have:

$$\begin{align*} &n_1+n_2+\ldots+n_k=n\\ \Rightarrow\ &(n_1-1)+(n_2-2)+\ldots+(n_k-1)=n-k\\ \Rightarrow\ &\sum^k_{i=1}(n_i-1)=n-k \end{align*}$$

On squaring both sides we get:

$$\begin{align*} &\left(\sum^k_{i=1}(n_i-1)\right)^2=(n-k)^2\\ \Rightarrow\ &\sum^k_{i=1}n_i^2-2\sum^k_{i=1}n_i+k+\text{Cross Term}_+=n^2-2nk+k^2\\ \Rightarrow\ &\sum^k_{i=1}n^2\le n^2-2nk+k^2+2n-k \end{align*}$$

On removing the non-negative cross term, we get:

$$\begin{align*} \sum^k_{i=1}n^2\le n^2-(k-1)(2n-k)&&&&&&&&&&(1) \end{align*}$$

The maximum number of edges in the $i^\text{th}$ component is $\frac{1}{2}n_i(n_i-1)$. Therefore, the maximum number of edges in the graph $G$ is equal to:

$$\begin{align*} \sum^k_{i=1}\frac{1}{2}n_i(n_1-1)&=\frac12\sum^k_{i=1}n_i^2-\frac12\sum^k_{i=1}n_i\\ \Rightarrow E_m&\le\frac12[n^2-(k-1)(2n-k)-n]&&[\text{From eq. (1)}]\\ \Rightarrow E_m&\le\frac12(n^2-2nk+k^2+2n-k-n)\\ \Rightarrow E_m&\le\frac12[(n-k)^2+(n-k)]\\ \Rightarrow E_m&\le\frac12(n-k)(n-k+1) \end{align*}$$

Taking the maximum value from above, we can state a simple graph with $n$ vertices and $k$ components can have at most, $E_m$ edges as stated below:

$$E_m=\frac12(n-k)(n-k+1)$$

Hence the theorem is proved.

16. Prove using propositional logic:

• (i) $(p\rightarrow r)\vee(q\rightarrow r)\equiv(p\wedge q)\rightarrow r$
• (ii) $p\leftrightarrow q\equiv(p\wedge q)\vee(\neg p\wedge\neg q)$

(i) Given: $(p\rightarrow r)\vee(q\rightarrow r)\equiv(p\wedge q)\rightarrow r$

$$\begin{align*} \text{LHP}&=(p\rightarrow r)\vee(q\rightarrow r)\\ &=(\neg p\vee r)\vee(\neg q\vee r)&&[\because a\rightarrow b=\neg a\vee b]\\ &=(\neg p\vee\neg q)\vee(\neg r\vee\neg r)&&[\because\text{associative}]\\ &=\neg(p\wedge q)\vee r&&[\text{De-Morga's law}]\\ &=(p\wedge q)\rightarrow r&&[\because a\rightarrow b=\neg a\vee b]\\ &=\text{RHP} \end{align*}$$

Hence proved.

(ii) Given: $p\leftrightarrow q\equiv(p\wedge q)\vee(\neg p\wedge\neg q)$

$$\begin{align*} \text{LHP}&=p\leftrightarrow q\\ &=(p\rightarrow q)\wedge(q\rightarrow p)\\ &=(\neg p\vee q)\wedge (\neg q\vee p)&&[\because a\rightarrow b=\neg a\vee b]\\ &=[(\neg p\vee q)\wedge\neg q]\vee[(\neg p\vee q)\wedge p]\\ &=[(\neg p\wedge\neg q)\vee(q\wedge\neg q)]\vee[(\neg p\wedge p)\vee(q\wedge p)]\\ &=[(\neg p\wedge \neg q)\vee F]\vee[F\vee(p\wedge q)]\\ &=(p\wedge q)\vee(\neg p\wedge \neg q)&&[\because a\vee F=a]\\ &=\text{RHP} \end{align*}$$

Hence proved.